Auxiliary field quantum Monte Carlo in the PAW method
Many-body methods are so expensive, because matrices with four indices need to be stored.
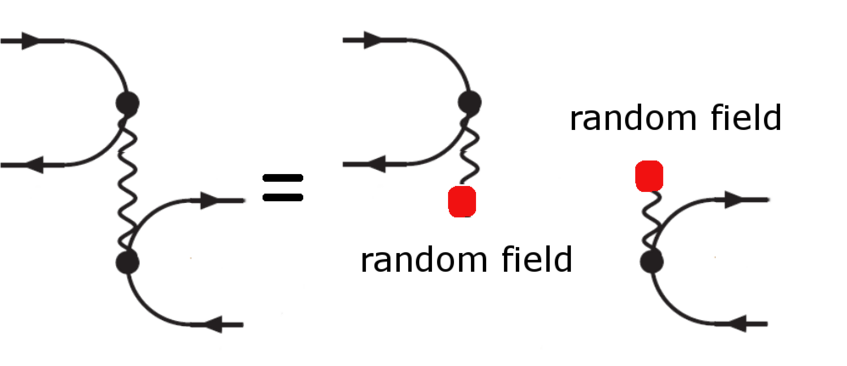
The AF-QMC replaces the Coulomb line by random fields (daemons) reducing the complexity
from four index quantities to three index quantities. This allows to significantly accelerate
quantum Monte Carlo algorithms.
Auxiliary field quantum Monte Carlo in the PAW method
Auxiliary field quantum Monte Carlo in the PAW method
Georg Kresse
Density functional theory (DFT) is undoubtedly the best-established method for making predictions about solids and materials. This is because the method is both very efficient and relatively accurate. However, the known approximations for the density functionals very often lead to uncontrollable errors, especially when chemical processes take place, i.e. if bonds are broken or reformed. Among other things, the so important energy barriers in catalytic processes are hence often described inaccurately. Therefore, for many years, methods have been worked on to determine the exact wave function and the exact energy of the multi-electron Schrödinger equation. This is an exceedingly difficult task, as the wave function is so complex that even the most powerful supercomputers in the world cannot store it. The second important aspect to consider is that the computing power of these supercomputers is constantly increasing, but no longer due to an increase in the power of the individual processors, but by increasing the number of processors. These two problems can only be solved conclusively using Monte-Carlo methods.
In this proposal the so-called auxiliary field quantum Monte Carlo (AF-QMC) method for Fermions shall be implemented and materials properties predicted. The AF-QMC is a relatively novel and not yet widely used method but it has numerous properties that make it particularly attractive. On the one hand, the individual calculation steps are very elementary, not dissimilar to those in the density functional theory mentioned above, so that the memory requirements remain low and we can reuse our expertise in DFT. On the other hand, the individual calculations can be easily distributed among thousands of processors, making the algorithm ideally suited for next-generation supercomputers (Austria has just become a member of PRACE and thus also has access to such computers).
After successful implementation and extensive testing of the method on simple solids, we will apply it to prototypical but important problems. We want to concentrate on the adsorption of molecules on solids, which is important for catalysis, as well as on correlated solids that can hardly be described with traditional methods now. We expect major breakthroughs in materials modelling using the here implemented methods.
The team: Currently we have three FWF funded collaborators on the team, Amir Taheridehkordi (PostDoc), Zoran Sukurma (PhD student), and Moritz Humer (Master student). Furthermore, Martin Schlipf from the VASP Software GmbH assists in the supervision of the project. If you want to join the team, please send an application to georg.kresse@univie.ac.at with the following information: (i) a curriculum vitae with full academic records, (ii) a motivation letter of one page, and (iii) a list of publications and papers, including one or two reprints representative of previous research.
Progress: We are still in the early stages of the project. Many of the essential pieces are in place, such as time propagation, estimating the correlation energy, and we are currently comparing result to a code developed by Zoran Sukurma for atoms. The most exciting aspect of the project is that we pursue low scaling methods using fast Fourier transformations. This will ultimately allow us to perform calculations on large systems with a much better scaling than methods relying on an explicit storage of two-electron four integrals. We expect this project to be a game changer for correlated wave function calculations! Stay tuned or join us now.
